Fungsi Kuadrat Dan Grafiknya

Fungsi Kuadrat dan Grafiknya

A. Bentuk umum fungsi kuadrat

B. Menenetukan persamaan grafik fungsi kuadrat

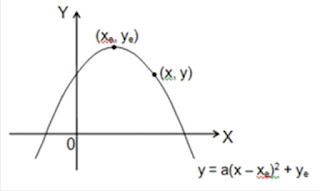
1). Grafik fungsi kuadrat yang melalui titik balik  dan sebuah titik tertentu 

2). Grafik fungsi kuadrat yang memotong sumbu X di dua titik  , dan melaui sebuah titik tertentu (x, y).

C. Kedudukan Fungsi Kuadrat terhadap Sumbu x

1. Jika a > 0 dan D > 0 maka parabola terbuka ke atas dan memotong sumbu x di dua titik
2. Jika a > 0 dan D = 0 maka parabola terbuka ke atas dan menyinggung sumbu x
3. Jika a > 0 dan D < 0 maka parabola terbuka ke atas dan tidak memotong maupun menyinggung sumbu x
4. Jika a < 0  dan D > 0 maka parabola terbuka ke bawah dan memotong sumbu x di dua titik
5. jika a < 0 dan D = 0 maka parabola terbuka ke bawah dan menyinggung sumbu x
6. Jika a < 0 dan D < 0 maka parabola terbuka ke bawah dan tidak memotong maupun menyinggung sumbu x 

D. Kedudukan Garis Terhadap Kurva Parabola

Kedudukan garis g : y = mx + n dan parabola  ada tiga kemungkinan seperti pada gambar berikut ini.

E. Teorema Fungsi Kuadrat

Dimisalkan garis g : y = mx + n dan parabola . Apabila persamaan garis g disubstitusikan ke persamaan parabola h, maka akan diperoleh sebuah persamaan kuadrat baru yaitu :

, Persamaan kuadrat baru

Determinan dari persamaan kuadrat baru tersebut adalah:

dengan melihat nilai deskriminan persamaan kuadrat baru tersebut akan dapat diketahui kedudukan garis g terhadap parabola h tanpa harus digambar grafiknya terlebih dahulu yaitu:

1. Jika D > 0, maka persamaan kuadrat memiliki dua akar real, sehingga garis g memotong parabola h di dua titik berlainan.

2. Jika D = 0, maka persamaan kuadrat memiliki dua akar kembar, sehingga garis g menyinggung parabola h

3. Jika D < 0, maka persamaan kuadrat tidak memiliki akar real, sehingga garis g tidak memotong ataupun menyinggung parabola h

F. Sketsa Grafik Fungsi Kudrat

Sketsa grafik suatu fungsi kuadrat   dapat digambarkan dengan langkah-langkah sebagai berikut:

Langkah 1

Tentukan titik potong dengan sumbu koordinat:

(a) Memotong sumbu x, jika f(x) = 0

(b) Memotong sumbu y, jika x = 0

Langkah 2

(a) Tentukan persamaan sumbu simetri 

<

(b) Tentukan titik puncak atau titik balik 

Langkah 3

Gunakan titik bantu jika perlu

Contoh

Gambarlah sketsa grafik fungsi kuadrat:




Jawab
Berdasarkan rumus di atas, cara menjawab fungsi kuadrat pada soal ini ada beberapa langkah, yaitu: 

Langkah 1
(a). Titik potong dengan sumbu x, maka y = 0



(x - 2) (x - 1) = 0
x = 2 atau x = 1

Jadi titik potongnya adalah (2, 0) dan (1, 0)


(b) Titik potong dengan sumbu y, maka x = 0



Jadi titik potongnya adalah (0, 2)


Langkah 2
(a) Persamaan sumbu simetri

(b) Koordinat titik puncak

Langkah 3

Gambar sketsa grafik, seperti pada grafik di bawah ini.

G. Menyusun Fungsi Kuadrat

Grafik fungsi kuadrat memotong sumbu x di  dan  serta melalui sebuah titik tertentu. Persamaan fungsi kuadratnya dapat dinyatakan sebagai:

Grafik fungsi kuadrat menyinggung sumbu x di  dan melalui sebuah titik tertentu. Persamaan fungsi kuadratnya dapat dinyatakan sebagai:

Grafik fungsi kuadrat melalui titik puncak atau titik balik  dan melalui sebuah titik tertentu. Persamaan fungsi kuadratnya dapat dinyatakan sebagai:

Grafik fungsi kuadrat melalui titik-titik , , dan . Persamaan fungsi kuadratnya dapat dinyatakan sebagai berikut:

 

Contoh

Soal No 1

Sebuah fungsi kuadrat memotong sumbu x di A (1, 0) dan B (2, 0). Jika fungsi kuadrat itu melalui titik (0, 4) tentukanlah persamaan fungsi kuadrat itu?

Jawab



Fungsi kuadrat melalui sumbu x memotong di titik A(1, 0) dan B(2, 0) maka:
y = a(x - 1) (x - 2) dan melalui titik (0, 4), sehingga

4 = a(0 - 1)(0 - 2)
4 - 2a
a = 2

Jadi persamaan fungsi kuadratnya adalah:

y = f(x) = 2 (x - 1)(x - 2)

y = f(x) = 



Soal No 2
Tentukan persamaan fungsi kuadrat yang mempunyai titik puncak  melalui titik 

Jawab



Persamaan fungsi kuadrat yang berpuncak di  adalah: 

Melalui titik , maka:

Jadi persamaan fungsi kuadratnya adalah:

Sebagai bahan evaluasi silahkan kerjakan soal-soal fungsi kuadrat di bawah ini.

Latihan Soal - Soal Fungsi Kuadrat

1) Persamaan grafik fungsi kuadrat yang mempunyai titik balik (1, -4) dan melalui titik (2, -3) adalah . . . .







2) Grafik fungsi kuadrat yang persamaannya adalah y = 6 + px -5x memotong sumbu x. Salah satu titik potongnya adalah (-2, 0) maka nilai p adalah . . . .

(a)  -13
(b) -7
(c) 6
(d) 7
(e) 13

3) Koordinat titik balik dari  adalah . . . .
(a) (-1,4)
(b) (1, 4)
(c) (1, -4)
(d) (-1, -4)
(e) (4, 1)


Gambarlah grafik fungsi

4) 

5) 

Tweet

Subscribe to receive free email updates: